Drawing consists of construction of primitive geometric forms
viz. points, lines and planes that serve a the building blocks for more
complicated geometric shapes and defining the position of object in space.
The use of lines for obtaining the drawing of planes is shown in
figure 1.
Figure 1 illustrates various
planes generally encountered
Solids are obtained by combination of planes. Plane surfaces of
simple solids are shown in figure 2.
Figure 2 surfaces of few
simples solids .
In addition curved surfaces also
exists. Figure 3 shows some of solids having curved surfaces.
Primitive geometric forms
The shapes of objects are formed from primitive geometric forms . These are
The shapes of objects are formed from primitive geometric forms . These are
1. Point
1. Line
2. Plane
3. Solid
4. Doubly curved
surface and object
5. Warped surface
The basic 2-D geometric
primitives, from which other more complex geometric forms are derived.
·
Points,
·
Lines,
·
Circles, and
·
Arcs
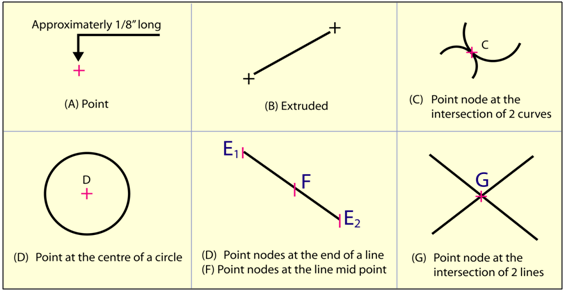
Point
A point is a theoretical location
that has neither width, height, nor depth and describes exact location in
space. A point is represented in technical drawing as a small cross made of
dashes that are approximately 3 mm long. As shown in figure 4, a
point is used to mark the locations of centers and loci, the intersection
ends, middle of entities
Figure 4. shows the various use of
points.
Line
A line is a geometric primitive that
has length and direction, but no thickness. Lines may be straight, curved or a
combination of these. As shown in figure 5, lines have few important
relationship or conditions, such as parallel, intersecting, and tangent.
Lines can be of specific length or non-specific length. A Ray is a sStraight
line that extends to infinity from a specified point.
Figure 5. Relationship of one line to
another line or arc
Bisecting a line
The procedure of bisecting a given
line AB is illustrated in figure 6.
With A as centre and radius equal to higher than half AB, draw two arcs. With B as centre and with the same radius draw another arc intersecting the preious arcs. The line joining the intersection points is the perpendicular bisector of the line AB.
With A as centre and radius equal to higher than half AB, draw two arcs. With B as centre and with the same radius draw another arc intersecting the preious arcs. The line joining the intersection points is the perpendicular bisector of the line AB.
Figure 6. Illustrates the method of
bisecting a line
Dividing a line into equal parts
The method of dividing a line MO into
equal number of parts is illustrated in figure 7.
·
Draw a line MO at any convenient angle (preferably an acute angle) from
point M.
·
From M and along MO, cut off with a divider equal divisions (say three)
of any convenient length.
·
Draw a line joining ON.
·
Draw lines parallel to MO through the remaining points on line MO.
The intersection of these lines with line MN will divide the line into
(three) equal parts.
Figure 7. Dividing a line in to equal
number of parts.
Planar tangent condition exists when
two geometric forms meet at a single point and do not intersect. This is self
explanatory from figure 8.
Figure 8. Illustrates the existence
of planar tangent condition.
Locating tangent points on circle and
arcs
The method of locating tangent points
on circle and arcs as well as thhe common tangent to two circles are
shown in figure 9(a) and (b) .
Figure 9. Locating the tangent points
to arcs or circles.
Drawing an arc tangent to a given
point on the line
The steps for drawing the arc tangent to a given point on a line is shown in figure 10.
The steps for drawing the arc tangent to a given point on a line is shown in figure 10.
1. Given line AB and
tangent point T. Construct a line perpendicular to line AB and through point T.
2. Locate the center
of the arc by making the radius on the perpendicular line. Put the point of the
compass at the center of the arc, set the compass for the radius of the arc,
and draw the arc which will be tangent to the line through the point T.
Figure 10. Drawing an arc tangent to
the a given point on a line.
Drawing an arc, tangent to two lines
The steps used to drawn an arc
tangent to two lines is illustrated in figure 11.
Figure 11. illustrates the method of
drawing an arc tangent to two lines.
Drawing an arc, tangent to a
line and an arc
Figure 12 shows the steps in drawing
an arc tangent to a line and an arc that (a) that do not intersect
and (b) that intersect each other.
Figure 12 Drawing an arc tangent to a
line and an arc
Construction of Regular Polygon of
given length AB
To construct a regular polygon with
length of edge AB us shown in figure 1.
Figure 1. Construction of a regular
polygon with a given length of edge.
·
Draw a line of length AB. With A as centre and radius AB, draw a
semicircle.
·
With the divider, divide the semicircle into the number of sides
(example of number of side 7 is shown in figure 1) of the polygon.
·
Draw a line joining A with the second division-point 2.
·
The perpendicular bisectors of A2 and AB meet at O. Draw a circle with
centre O and radius OA.
·
With length A2, mark points F, E, D & C on the circumferences
starting from 2 (Inscribe circle method)
·
With centre B and radius AB draw an arc cutting the line A6 produced at
C. Repeat this for other points D, E & F (Arc method)
General method of drawing any polygon
A more general method of drawing any
polygon with a given length of edge is shown in figure 2.
·
Draw AB = given length of polygon
·
At B, Draw BP perpendicular & = AB
·
Draw Straight line AP
·
With center B and radius AB, draw arc AP.
·
The perpendicular bisector of AB meets the line AP and arc AP in 4 and 6
respectively.
·
Draw circles with centers as 4, 5,&6 and radii as 4B, 5B, & 6B
and inscribe a square, pentagon, & hexagon in the respective circles.
·
Mark point 7, 8, etc with 6-7,7-8,etc. = 4-5 to get the centers of
circles of heptagon and octagon, etc.
Figure 2 Drawing any polygon with a
given length of edge
Inscribe a circle inside a regular
polygon
The method of inscribing a circle
inside a regular polygon is illustrated in figure 3.
1. Bisect any two
adjacent internal angles of the polygon.
2. From the
intersection of these lines, draw a perpendicular to any one side of the
polygon (say OP).
3. With OP as radius,
draw the circle with O as cente
Figure 3 Inscribing a circle inside a
regular polygon
Inscribe a regular polygon of any
number of sides (say n = 5), in a circle
Figure 4 shows the method of
inscribing a regular polygon of any number of sides.
·
Draw the circle with diameter AB.
·
Divide AB in to “n” equal parts
·
Number them.
·
With center A & B and radius AB, draw arcs to intersect at P.
·
Draw line P2 and produce it to meet the circle at C.
·
AC is the length of the side of the polygon.
Figure 4 Inscribing a regular polygon
of any number of sides.
To draw a circle to touch a given
line, and a given circle at a given point on it.
The method is illustrated in figure
5.
·
Given: Line AB, circle with centre C
and point P on the circle.
·
From P, draw a tangent to the circle intersecting AB at D.
·
Draw bisector of angle PDB to intersect the line through C and P
at O.
·
With center O and radius OP, draw the required circle.
Figure 5. shows the method of
drawing a circle to touch a given line and a given circle at a particular
point.
Inside a regular polygon, draw the
same number of equal circles as the side of the polygon,each circle touching
one side of the polygon and two of the other circles
The technique is shown in figure 6
·
Draw bisectors of all the angles of the polygon, meeting at O, thus
dividing the polygon into the same number of triangles.
·
In each triangle inscribe a circle.
Figure 6. Drawing the same
number of equal circles, in a given polygon , as the side of the polygon
Figure 7 shows the technique
for drawing the same number of equal circles as the side of the polygon inside
a regular polygon, each circle touching two adjacent sides of the polygon and
two of the other circles.
·
Draw the perpendicular bisectors of the sides of the polygon to obtain
same number of quadrilaterals as the number of sides of the
polygon.
·
Inscribe a circle inside each quadrilateral.
Figure 7. drawing the same number of
equal circles as the side of the polygon inside a regular polygon
Figure 8 shows the method of drawing
a circle touching three lines inclined to each other but not forming a
triangle.
·
Let AB, BC, and AD be the lines.
·
Draw bisectors of the two angles, intersecting at O.
·
From O draw a perpendicular to any one line intersecting it at P.
·
With O as center and OP as radius draw the desired circle.
Figure 9 shows the method of drawing
outside a regular polygon, the same number of equal circles as the sides
of the polygon, each circle touching one side of the polygon and two of the
other circles.
·
Draw bisectors of two adjacent angles and produce them outside the
polygon.
·
Draw a circle touching the extended bisectors and the side AB (in this
case) and repeat the same for other sides.
Figure 9 shows the method of drawing
outside a regular polygon, the same number of equal circles as the sides
of the polygon,





















No comments:
Post a Comment