Limits and Tolerences for Design

Design and Manufacturing

A machine element, after design, requires to be manufactured to give it a shape of a product. Therefore, in addition to standard design practices like, selection of proper material, ensuring proper strength and dimension to guard against failure, a designer should have knowledge of basic manufacturing aspects.

In this lesson, we will discuss briefly about some of the basic manufacturing requirements and processes.

First and foremost is assigning proper size to a machine element from manufacturing view point. As for example, a shaft may be designed to diameter of, say, 40 mm. This means, the nominal diameter of the shaft is 40 mm, but the actual size will be slightly different, because it is impossible to manufacture a shaft of exactly 40 mm diameter, no matter what machine is used. In case the machine element is a mating part with another one, then dimensions of both the parts become important, because they dictate the nature of assembly. The allowable variation in size for the mating parts is called limits and the nature of assembly due to such variation in size is known as fits.

Limits

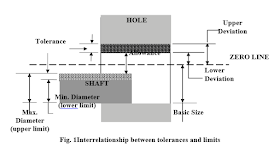
Fig. 1 explains the terminologies used in defining tolerance and limit. The zero line, shown in the figure, is the basic size or the nominal size. The definition of the terminologies is given below. For the convenience, shaft and hole are chosen to be two mating components.

Tolerance

Tolerance is the difference between maximum and minimum dimensions of a component, ie, between upper limit and lower limit. Depending on the type of application,  the  permissible  variation  of  dimension  is  set  as  per  available standard grades.

  

Tolerance is of two types, bilateral and unilateral. When tolerance is present on both sides of nominal size, it is termed as bilateral; unilateral has tolerance only on one side.

Allowance

It is the difference of dimension between two mating parts.

Upper deviation

It is the difference of dimension between the maximum possible size of the component and its nominal size.

Lower deviation

Similarly, it is the difference of dimension between the minimum possible size of the component and its nominal size.

Fundamental deviation

It defines the location of the tolerance zone with respect to the nominal size. For that matter, either of the deviations may be considered.

Fit System

We have learnt above that a machine part when manufactured has a specified tolerance. Therefore, when two mating parts fit with each other, the nature of fit is dependent on the limits of tolerances and fundamental deviations of the mating parts. The nature of assembly of two mating parts is defined by three types of fit system, Clearance Fit, Transition Fit and Interference Fit. The fit system is shown schematically in Fig.3.

There are two ways of representing a system. One is the hole basis and the other is the shaft basis. In the hole basis system the dimension of the hole is considered to be the datum, whereas, in the shaft basis system dimension of the shaft is considered to be the datum.  The holes are normally made by drilling, followed by reaming. Therefore, the dimension of a hole is fixed due to the nature of the tool used. On the contrary, the dimension of a shaft is easily controllable by standard manufacturing processes. For this reason, the hole basis system is much  more  popular  than  the  shaft  basis  system.  Here,  we  shall  discuss  fit system on hole basis.

Clearance Fit

In this type of fit, the shaft of largest possible diameter can also be fitted easily even in the hole of smallest possible diameter.

Transition Fit

In this case, there will be a clearance between the minimum dimension of the shaft and the minimum dimension of the hole. If we look at the figure carefully, then  it  is  observed  that  if  the  shaft  dimension  is  maximum  and  the  hole dimension is minimum then an overlap will result and this creates a certain amount of tightness in the fitting of the shaft inside the hole. Hence, transition fit may have either clearance or overlap in the fit.

Interference Fit

In this case, no matter whatever may be the tolerance level in shaft and the hole, there is always a overlapping of the matting parts. This is known as interference fit. Interference fit is a form of a tight fit.

Standard limit and fit system

Fig. 4 shows the schematic view of a standard limit and fit system. In this figure tolerance is denoted as IT and it has 18 grades; greater the number, more is the tolerance limit. The fundamental deviations for the hole are denoted by capital letters from A and ZC, having altogether 25 divisions. Similarly, the fundamental deviations for the shaft is denoted by small letters from a to zc.

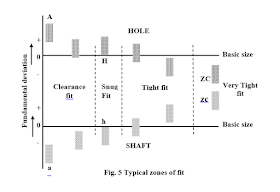
Here H or h is a typical case, where the fundamental deviation is zero having an unilateral tolerance of a specified IT grade.

Therefore in standard limits and fit system we find that, Standard tolerances

18 grades: IT01, IT0 and IT1-1T16

Fundamental deviations

25 types: A- ZC (For holes)

a- Zc (For shafts)

The values of standard tolerances and fundamental deviations can be obtained by consulting design hand book. It is to be noted that the choice of tolerance grade is related to the type of manufacturing process; for example, attainable tolerance grade for lapping process is lower compared to plain milling. Similarly, choice of fundamental deviation largely depends on the nature of fit, running fit or tight fit etc. The approximate zones for fit are shown in Fig.5. Manufacturing processes involving lower tolerance grade are generally costly. Hence the designer has to keep in view the manufacturing processes to make the design effective and inexpensive.

Sample designation of limit and fit,  50H6/g5.

The designation means that the nominal size of the hole and the shaft is 50 mm. H is the nature of fit for the hole basis system and its fundamental deviation is zero. The tolerance grade for making the hole is IT6.  Similarly, the shaft has the fit type g, for which the fundamental deviation is negative, that is, its dimension is lower than the nominal size, and tolerance grade is IT5.

Common manufacturing processes

The types of common manufacturing processes are given below in the Fig.6

The types of shaping processes are given below in the Fig. 7.

Following are the type of machining processes, shown in Fig. 8.

Various joining processes are shown in Fig. 9.

The surface finishing processes are given below (Fig.10).

The non-conventional machining processes are as follows (Fig.11),