Flywheel
A flywheel is an inertia energy-storage member of engine. It absorb mechanical rotational energy and serves as a energy reservoir, storing energy during the power stroke when the supply of energy is more than the requirement and releases it during the idle stroke when the requirement of energy is more than the supply.
Flywheels Function need and Operation
The main function of a fly wheel is to smoothen out variations in the speed of a shaft caused by torque fluctuations. If the source of the driving torque or load torque is fluctuating in nature, then a flywheel is usually called for. Many machines have load patterns that cause the torque time function to vary over the cycle. Internal combustion engines with one or two cylinders are a typical example. Piston compressors, punch presses, rock crushers etc. are the other systems that have fly wheel. Flywheel absorbs mechanical energy by increasing its angular velocity and delivers the stored energy by decreasing its velocity.
Design Approach
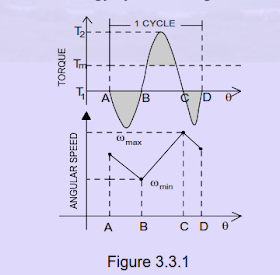
There are two stages to the design of a flywheel. First, the amount of energy required for the desired degree of smoothing must be found and the (mass) moment of inertia needed to absorb that energy determined. Then flywheel geometry must be defined that caters the required moment of inertia in a reasonably sized package and is safe against failure at the designed speeds of operation. Design Parameters Flywheel inertia (size) needed directly depends upon the acceptable changes in the speed. Speed fluctuation The change in the shaft speed during a cycle is called the speed fluctuation and is equal to ω max - ω min
Fl = ω max - ω min
We can normalize this to a dimensionless ratio by dividing it by the average or nominal shaft speed (ωave) .
cf= (ωmax −ωmin)/ω
Where ωavg is nominal angular velocity
Co-efficient of speed fluctuation
The above ratio is termed as coefficient of speed fluctuation Cf.
Where ω is nominal angular velocity, and ω the average or mean shaft speed desired. This coefficient is a design parameter to be chosen by the designer.
The smaller this chosen value, the larger the flywheel have to be and more the cost and weight to be added to the system. However the smaller this value more smoother the operation of the device It is typically set to a value between 0.01 to 0.05 for precision machinery and as high as 0.20 for applications like crusher hammering machinery.
The above equation can be used to obtain appropriate flywheel inertia corresponding to the known energy change E k for a specific value coefficient of speed fluctuation Cf ,
Thus the mass moment of inertia I m needed in the entire rotating system in order to obtain selected coefficient of speed fluctuation is determined using the relation
Torque Variation and Energy
The required change in kinetic energy E is obtained from the known torque time relation or curve by integrating it for one cycle.
Torque Time Relation without Flywheel
A typical torque time relation for example of a mechanical punching press without a fly wheel in shown in the figure. In the absence of fly wheel surplus or positive enregy is avalible initially and intermedialty and enery absorbtion or negative energy during punching and stripping operations. A large magitidue of speed fluctuation can be noted. To smoothen out the speed fluctuation fly wheel is to be added and the fly wheel energy needed is computed as illustrated below
Torque Time Relation with Flywheel
Geometry of Flywheel
The geometry of a flywheel may be as simple as a cylindrical disc of solid material, or may be of spoked construction like conventional wheels with a hub and rim connected by spokes or arms Small fly wheels are solid discs of hollow circular cross section. As the energy requirements and size of the flywheel increases the geometry changes to disc of central hub and peripheral rim connected by webs and to hollow wheels with multiple arms.
The latter arrangement is a more efficient of material especially for large flywheels, as it concentrates the bulk of its mass in the rim which is at the largest radius. Mass at largest radius contributes much more since the mass moment of inertia is proportional to mr^2
Stresses in Flywheel
Flywheel being a rotating disc, centrifugal stresses acts upon its distributed mass and attempts to pull it apart. Its effect is similar to those caused by an internally pressurized cylinder.
γ = material weight density, ω= angular velocity in rad/sec. ν= Poisson’s ratio, is the
radius to a point of interest, ri and r are inside and outside radii of the solid disc flywheel.
Analogous to a thick cylinder under internal pressure the tangential and radial stress in a solid disc flywheel as a function of its radius r is given by:
The point of most interest is the inside radius where the stress is a maximum. What causes failure in a flywheel is typically the tangential stress at that point from where fracture originated and upon fracture fragments can explode resulting extremely dangerous consequences, Since the forces causing the stresses are a function of the rotational speed also, instead of checking for stresses, the maximum speed at which the stresses reach the critical value can be determined and safe operating speed can be calculated or specified based on a safety factor. Generally some means to preclude its operation beyond this speed is desirable, for example like a governor. Consequently











No comments:
Post a Comment